Answer:
The equation of the ellipse is
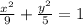
Explanation:
Let the equation of the ellipse is
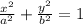 {As the center of the ellipse is at the origin}
{As the center of the ellipse is at the origin}
Therefore, the vertices of the ellipse are (± a,0) and foci are (± ae,0)
Now, given that a = 3 and ae = 2
Now, eccentricity of a ellipse is given by b² = a² - a²e² = 3² - 2² = 5
Therefore, the equation of the ellipse is
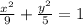 (Answer)
(Answer)