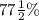Question

Covert 77 1/2% to a fraction in lowest term

Answer 1

`77(1)/(2) \%` converted to fraction in lowest terms is
`(31)/(40)`

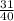
Solution:

Given that we have to convert
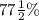`77(1)/(2) \%` to fraction in lowest terms

Let us first convert the mixed fraction
`77(1)/(2)`

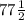
Multiply the whole number part by the fraction's denominator.

Add that to the numerator.

Then write the result on top of the denominator.

Therefore,

`77(1)/(2) \% = (77 * 2+1)/(2) \% = (155)/(2) \%`

`(155)/(2) \% = 77.5 \%`

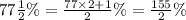
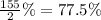
Now convert 77.5 % to fraction

So we have to convert percentage to fraction

Divide the percentage by 100 to get a decimal number

`77.5 \% = (77.5)/(100) = 0.775`

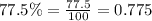
Use that decimal number as the numerator of a fraction. Put a 1 in the denominator of the fraction

Count the number of places to the right of the decimal. If you have x decimal places then multiply numerator and denominator by
`10^x`

`0.775 = (0.775)/(1) * (1000)/(1000) = (775)/(1000)`

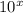
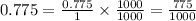
Simplify and reduce the fraction to lowest terms

`\rightarrow (775)/(1000) = (31)/(40)`

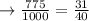
Thus the given percentage is converted to fraction in lowest terms