Question

Two candles of equal length are lit at the same time. One candle takes 6 hours to burn out, and the other takes 9 hours to burn out. After how much time will the slower burning candle be exactly twice as long as the faster burning one?

Answer 1

4.5 hours

Explanation:

Given: One candle takes 6 hour to burn out

Other candle takes 9 hours to burn out.

Lets assume the time at which slower burning candle be exactly twice as long as the faster burning one be "x". and lenght of candle initially be "1".

Taking one candle as Candle A

Other candle as Candle B.

As given both the candle is of equal length.

Now, putting up the equation to find the time at which lenght of candle B is twice as candle A.

∴ Length of candle=
`2(1-(x)/(6) )= (1-(x)/(9))`

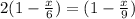
Solving it knowing length is constant and using distributive property of multiplication

⇒
`2-(2x)/(6) = 1-(x)/(9)`

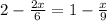
subtracting both side by 2

⇒
`(-2x)/(6) = -1 -(x)/(9)`

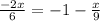
Adding both side by
`(x)/(9)`

⇒
`-(2x)/(6) +(x)/(9) = -1`

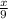
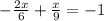
Taking LCD of 9 and 6 as 18

⇒
`(-2x* 3+x* 2)/(18)= -1`

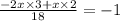
Multiplying both side by 18

⇒
`-6x+2x= -18`

⇒
`-4x= -18`

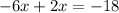
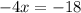
Multiplying both side by -4

⇒ x=
`(-18)/(-4)= (9)/(2)`

∴ x= 4.5 hours

Hence, 4.5 hours is the time at which slower burning candle be exactly twice as long as the faster burning one.