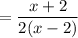Question

Please show your work and explain it.

Answer 1

`f(x)=(x+2)/(2(x-2))`

Explanation:

Remember when you divide fractions, you need to get the reciprocal of the divisor and multiply. So your first simplification would be:

`(x^2+4x+4)/(x^2-6x+8)/(6x+12)/(3x-12)\\\\=(x^2+4x+4)/(x^2-6x+8)*(3x-12)/(6x+12)\\\\=((x^2+4x+4)(3x-12))/((x^2-6x+8)(6x+12))`

Next we factor what we can so we can further simplify the rest of the equation:

`=((x^2+4x+4)(3x-12))/((x^2-6x+8)(6x+12))\\\\=((x+2)(x+2)(3x-12))/((x^2-6x+8)(6(x+2)))\\\\`

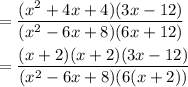
We can now cancel out (x+2)

`=((x+2)(3x-12))/((x^2-6x+8)(6))`

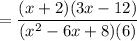
Next we factor out even more:

`=((x+2)(3)(x-4))/((x-2)(x-4)(6))`

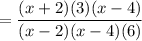
We cancel out x-4 and reduce the 3 and 6 into simpler terms:

`=((x+2)(1))/((x-2)(2))`

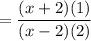
And we can now simplify it to:

`=(x+2)/(2(x-2))`