Question

Adaline is designing a garden in the shape of a 45º-45º-90º triangle, with an area of 32 ft2. To the nearest foot, how much fencing will she need to enclose the garden?

Answer 1

27 feet of fencing will be required to enclose the triangular garden.

Explanation:

Adaline is designing a garden in the shape of a 45º-45º-90º triangle, with an area of 32 ft².

So, the triangle is isosceles right triangle with, Base = Height = x ft. (Say)

So, the area of the triangle,
`(1)/(2) * (\textrm {Base}) * (\textrm {Height}) = 32`

⇒
`(1)/(2) x^(2) = 32`

⇒ x² = 64

⇒ x = 8 feet.

So, the hypotenuse =
`\sqrt{8^(2) + 8^(2)} = 8√(2) = 11.3` feet.

Therefore, the perimeter of the triangle will be = (8 + 8 + 11.3) = 27.3 ≈ 27 feet.

So, 27 feet of fencing will be required to enclose the triangular garden. (Answer)

Answer 2

27 ft

Explanation:

Given: A garden in the shape of a 45º-45º-90º triangle.

Area of triangle= 32 ft²

As given dimension of triangle, we understand that it is a right angle and triangle and since two angles are equal, therefore two sides of triangle are also equal.

∴ Base and height will be equal.

Assuming base is also as "h"

Now, finding the length of base and height by using area of triangle formula.

Area of triangle=
`(1)/(2) * base* height`

⇒
`32= (1)/(2) * h* h`

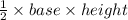
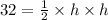
Multiplying both side by 2

⇒
`64= h^(2)`

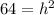
Square rooting both side, remember; √a²= a

⇒
`√(64) = h`

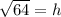
∴ h= 8 feet

Hence, both base and height of right angle triangle is 8 feet.

Next, finding total fencing required to enclose the garden.

Perimeter of garden is equal to the amount of fencing required by Adaline.

Therefore, finding the length of hypotenous of triangle too.

Using pythogorean theoram.

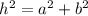`h^(2) = a^(2) +b^(2)`, where a is the height and b is the base of triangle.

⇒
`h^(2)= 8^(2) +8^(2)`

⇒
`h^(2) = 128`

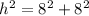
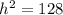
Square rooting both side

⇒
`h= √(128)`

∴ h= 11.3 feet

Perimeter of garden=
`base+height+hypotenous`

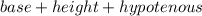
⇒ Perimeter of garden=
`8+8+11.3= 27.3\ feet`
`\approx 27\ feet`

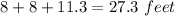
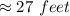
Hence, 27 feet fencing is required to enclose the garden.