Question

Jon is hitting baseballs. When he tosses the ball into the air, his hand is 5 feet above the ground. He hits the ball when it falls back to a height of 4 feet. The height of the ball is given by h = - 16x^2 + 6t + 5 where in seconds How much time will pass before Jon hits the ball? What is the maximum height the ball attains?

Answer 1

Time that will pass before Jon hits the ball is 0.5 seconds

The maximum height the ball attains is 6.875 feet

Explanation:

Step 1: To find out how much time passes before Jon hits the ball

The height he hits the ball when it falls is 4 feet

so,

`4 = - 16t^2 + 6t + 5`

`4 + 16t^2 - 6t - 5 = 0`

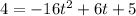
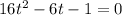`16t^2 - 6t -1 = 0` -------------------------(1)

Solving eq(1) using quadratic formula, we get

`t = (-b \pm√(b^2-4ac))/(2a)`

`t = (-(-6) \pm√((-6)^2-4(16)(-1)))/(2(16))`

`t = (6 \pm√(36+64))/(32)`

`t = (6 \pm√(100))/(32)`

`t = (6 \pm10)/(32)`

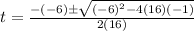
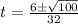
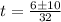
Taking only the positive value

`t = (16)/(32)`

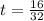
t = 0.5 seconds

Step 2: To find the maximum height of the ball

Max height will be reached at [
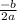`(-b)/(2a)`] sec

`=(-b)/(2a)`

`\\ = (-(-6))/(2*16)\\`

`= (6)/(32)`

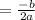
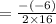
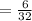
Now the height at t=
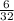`(6)/(32)` is

`16( (6)/(32))^2 - 6( (6)/(32)) -1 = h`

`( (6)/(2))^2 - (36)/(32) -1 = h`

`( 3)^2 - 1.125 -1 = h`

`9 - 1.125 -1 = h`

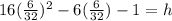
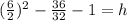
6.875 = h