Question

WORTH 75-100 POINTS YOU MUST ANSWER EACH QUESTION AND SHOW YOUR MATH

Tyler has $1000 that he wants to put in a savings account. He wants to save the money for 6 years. After 6 years he plans to take the money out and spend it on college. He looks at two different banks, and they offer him different interest options.

1. Bank A offers Tyler 4% simple interest. How much would Tyler’s investment be worth after 6 years in this account? Show your calculations below.

2. Bank B offers Tyler 3% interest compounded annually. How much would Tyler’s investment be worth after 6 years in this account? Show your calculations below.

3. In which bank should Tyler place the $1000 he is saving for college?

Tyler’s mom also has $1000 that she wants to put in a savings account. She is saving her money for retirement. She plans to retire in 30 years.

Tyler’s mom must also choose between Bank A and Bank B.

1. Bank A offers 4% simple interest. How much would Tyler’s mom’s investment be worth after 30 years in this account? Show your calculations below.

2. Bank B offers 3% interest compounded annually. How much would Tyler’s mom’s investment be worth after 30 years in this account? Show your calculations below

3. In which bank should Tyler’s mom place the $1000 she is saving for retirement?

4. Which interest rate is better for Tyler? Which is better for his mother? Explain the differences between the two. How can one interest rate be more advantageous to Tyler while a different one is more advantageous to his mother?

Answer 1

TYLER

1. Bank A: $1240

2. Bank B: $1194.05

3. Choose Bank A, simple interest at higher rate

TYLER'S MOM

1. Bank A: $2200

2. Bank B: $2427.26

3. Choose Bank B, compound interest at lower rate

4. The simple interest rate at 4% is better for Tyler, but the compound interest rate at 3% is better for Tyler's mom. Simple interest is calculated on the principal. Compound interest is calculated on the principal and the other interest that was earned. Over a longer period of time, the investment worth after compound interest will be worth more, even if the interest rate is lower. Since Tyler's mom has more time for her investment than Tyler, compound interest at a lower rate is more advantageous to her.

Step-by-step explanation:

For this problem, you need the formula to calculate amount after simple interest A = P(1 + rt)

"A" for amount (final worth of investment)

"P" for principal (starting investment)

"r" for interest rate in decimal form

"t" for time in years

You also need the formula for amount after compound interest A = P(1 + i)ⁿ

"A" for amount

"P" for principal

"i" for interest per compounding period, calculated using i = r/c

"n" for number of compounding periods, calculated by n = tc

"c" means how often interest is calculated. (Ex: annually = 1; quarterly = 4)

To solve the problems, substitute the known values into the equations.

FOR TYLER: P = 1000; t = 6

1. Use simple interest formula. r = 4% = 0.04 (converted to decimals)

A = P(1 + rt)

A = 1000(1 + (0.04)(6)) Substituted known values

A = 1000(1 + 0.24) Solved multiplication within brackets

A = 1000(1.24) Solved addition within brackets

A = 1240 Bank A future investment worth

Tyler's investment would be worth $1240 in Bank A.

2. Use compound interest formula. r = 3% = 0.03 (converted to decimals)

Calculate "i" and "n" inside the formula.

`A = P(1 + i)^(n)`

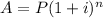
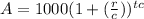`A = 1000(1 + ((r)/(c)))^(tc)` c = 1 because interest is calculated annually

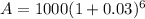`A = 1000(1 + 0.03)^(6)` Substituted known values.

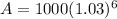`A = 1000(1.03)^(6)` Solved within brackets first.

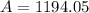`A = 1194.05` Rounded 1194.0523 to two decimal places

Tyler's investment would be worth $1194.05 in Bank B.

3. Tyler should place the $1000 he is saving for college in Bank A because he will have more money.

Bank A > Bank B

1240 > 1194.05

FOR TYLER'S MOM P = 1000; t = 30

1. Use simple interest formula. r = 4% = 0.04 (converted to decimals)

A = P(1 + rt)

A = 1000(1 + (0.04)(30)) Substituted known values

A = 1000(1 + 1.2) Solved multiplication within brackets first

A = 1000(2.2) Solved addition within brackets

A = 2200

Tyler's mom's investment would be worth $2200 from Bank A.

2. Use compound interest formula. r = 3% = 0.03 (converted to decimals)

Calculate "i" and "n" inside the formula.

`A = P(1 + i)^(n)`

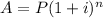
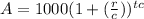`A = 1000(1 + ((r)/(c)))^(tc)` c = 1 because interest is calculated annually

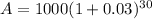`A = 1000(1 + 0.03)^(30)` Substituted known values

`A = 1000(1.03)^(30)` Solved within brackets first

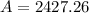`A = 2427.26` Rounded 2427.26247 to two decimal places

Tyler's mom's investment would be worth $2427.26 from Bank B.

3. Tyler's mom should place the $1000 she is saving for retirement in Bank B because she will have more money.

Bank A < Bank B

2200 < 2427.26

4. The simple interest rate at 4% is better for Tyler, but the compound interest rate at 3% is better for Tyler's mom. Simple interest is calculated on the principal. Compound interest is calculated on the principal and the other interest that was earned. Over a longer period of time, the investment worth after compound interest will be worth more, even if the interest rate is lower. Since Tyler's mom has more time for her investment than Tyler, compound interest at a lower rate is more advantageous to her.