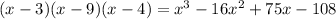Question

Joe is building a post for his mailbox. To find the correct dimensions, he needs to expand this expression: (x-3) (x-9) (x-4) Select the equivalent expression written in the format ax3(cubed) + bx2(squared) +cx+d

Answer 1

`(x-3)(x-9)(x-4)=x^3-16x^2+75x-108`

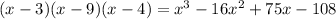
Explanation:

Given:

The expression to expand is given as:

`(x-3)(x-9)(x-4)`

Let us expand the first two binomials of the given expression using FOIL method.

The FOIL method states that:

`(a + b)(c + d) = ac + ad + bc + bd`

`(x-3)(x-9)=(x* x)+(x* -9)+(-3* x)+(-3* -9)\\\\(x-3)(x-9)=x^2-9x-3x+27=x^2-12x+27`

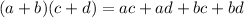
Now, let us multiply the result with the remaining binomial. Multiplying each term of the trinomial with each term of the binomial, we get:

`(x^2-12x+27)(x-4)\\\\= (x^2* x)+ (x^2* -4)+(-12x* x)+(-12x* -4)+(27* x)+(27* -4)\\\\=x^3-4x^2-12x^2+48x+27x-108\\\\=x^3-16x^2+75x-108...........(\because-12x^2-4x^2=-16x^2,48x+27x=75x)`

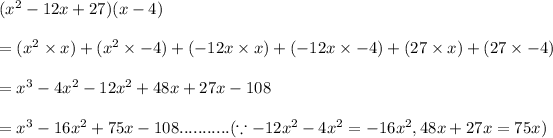
Therefore, the equivalent expression after expanding is given as:

`(x-3)(x-9)(x-4)=x^3-16x^2+75x-108`