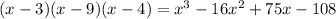Answer:
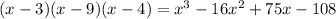
Explanation:
Given:
The expression to expand is given as:

Let us expand the first two binomials of the given expression using FOIL method.
The FOIL method states that:
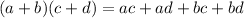
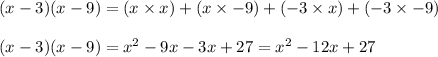
Now, let us multiply the result with the remaining binomial. Multiplying each term of the trinomial with each term of the binomial, we get:
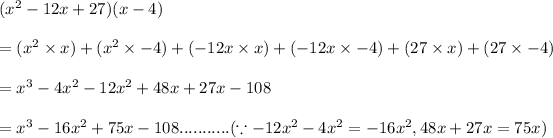
Therefore, the equivalent expression after expanding is given as: