Question

A cylinder and a cone have the same diameter: 8 inches. The height of the cylinder is 3 inches. The height of the cone is 18 inches

Use TT 3.14
What is the relationship between the volume of this cylinder and this cone? Explain your answer by determining the volume of each and comparing them. Show all your work

Answer 1

The relationship is that two times the volume of cylinder is volume of cone

Solution:

Given that, cylinder and a cone have the same diameter: 8 inches

Diameter = 8 inches

Radius is diameter divided by 2

`radius = (diameter)/(2)\\\\radius = (8)/(2) = 4`

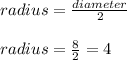
Radius = 4 inches

Let us find the volume of cylinder and cone

Volume of cylinder:

`volume = \pi r^2 h`

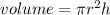
Radius = 4 inches

The height of the cylinder is 3 inches

height = 3 inches

Substituting the values, we get

`volume = 3.14 * 4^2 * 3\\\\volume = 3.14 * 16 * 3\\\\volume = 150.72`

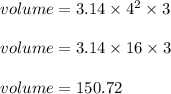
Thus volume of cylinder is 150.72 cubic inches

Volume of cone:

`volume = (\pi r^2h)/(3)`

Radius = 4 inches

The height of the cone is 18 inches

height = 18 inches

Substituting the values, we get

`volume = (3.14 * 4^2 * 18)/(3)\\\\volume = 3.14 * 16 * 6\\\\volume = 301.44`

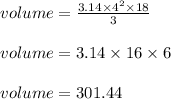
Thus volume of cone is 301.44 cubic inches

What is the relationship between the volume of this cylinder and this cone?

Volume of cylinder is 150.72 cubic inches

Volume of cone is 301.44 cubic inches

On observing the volume of cylinder and cone, we find that two times the volume of cylinder is volume of cone

`2 * \text{Volume of cylinder} = \text{Volume of cone}`

`2 * 150.72 = 301.44\\\\301.44 = 301.44`

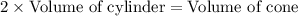
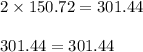
Thus the relationship between the volume of this cylinder and this cone is that two times the volume of cylinder is volume of cone