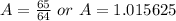Answer:
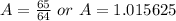
Step-by-step explanation:
Given:
The expression is given as:
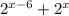
The equivalent expression to the above expression is given as:
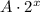
Now, simplifying the original expression using the law of indices:

So,
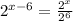 . The expression becomes:
. The expression becomes:
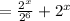
Now,
 is a common factor to both the terms, so we factor it out. This gives,
is a common factor to both the terms, so we factor it out. This gives,
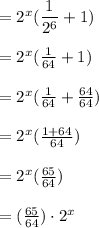
Now, on comparing the simplified form with the equivalent expression, we conclude:
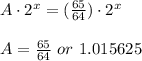
Therefore, the value of 'A' is