Explanation:
We begin with the function:
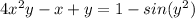
The first thing that we need to do is implicitly differentiate this function with respect to x.
Let us differentiate each piece individually and then combine them.
First,
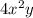
There are two thing that we need to keep in mind with this: we will need to apply a product rule and when we differentiate a y with respect to x, we are left with a
 .
.
![4x^2y\\4[(2xy)+(x^2(dy)/(dx))}]\\8xy+4x^2(dy)/(dx)](https://img.qammunity.org/2021/formulas/mathematics/high-school/2s3ydwugqt0gatue0l5ubiun185ojr7mjx.png)
Now,
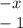
And now,
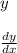
And lastly,
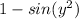
For this, we will need to apply the chain rule.
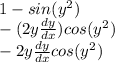
Now that we have differentiated each part of this function, we can combine them together to get
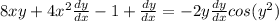
Our next course of action will be getting all of the terms with
 onto one side so that we can factor it out.
onto one side so that we can factor it out.
When this is done, we end up with

Once factored, we will get
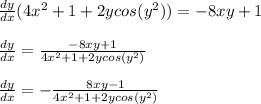
We then were able to isolate
 and then factor out a -1 from the numerator to get our final answer.
and then factor out a -1 from the numerator to get our final answer.
Regarding your answer, From what I can see, you ended up incorrectly factoring out the
 from each side before you moved all of the terms to one side. This does not work as there are terms that do not have
from each side before you moved all of the terms to one side. This does not work as there are terms that do not have
 that are having it factored out of them.
that are having it factored out of them.