Answer:
The total length (in units) of the biking trail is 15 units
Explanation:
Given:
P = (-2,1)
Q = (6, 1)
R = (6,-3)
s = (9,-3)
To Find:
The total length (in units) of the biking trail = ?
Solution:
Distance between two points can be found by the
d =
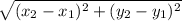 --------------(1)
--------------(1)
Step 1: Distance between PQ
Here
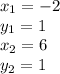
Substituting the values in eq(1)
PQ =

PQ =
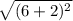
PQ =

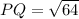
PQ = 8
Step 2: Distance between QR
Here
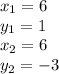
Substituting the values in eq(1)
QR =
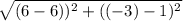
QR =
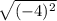
QR =
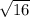
QR = 4
Step 3: Distance between RS
Here

Substituting the values in eq(1)
RS=
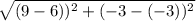
RS =

RS =
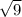
RS = 3
Step 4: Finding the total distance of the trail
The total distance of the biking trail is = PQ + QR + RS
=> 8+4+3
=> 15