Answer:
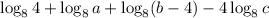
The equivalent expression is log Subscript 8 Baseline 4 + log Subscript 8 Baseline a + (log Subscript 8 Baseline (b minus 4) minus 4 log Subscript 8 Baseline c)
Explanation:
The expression is written as
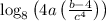
Using the log rule:
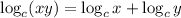 , the expression can be written as,
, the expression can be written as,
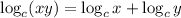
Using the log rule:
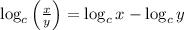 , the expression can be written as,
, the expression can be written as,
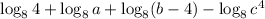
Since, we know that,
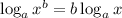 , the expression is written as,
, the expression is written as,
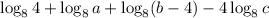
Thus, the equivalent expression is log Subscript 8 Baseline 4 + log Subscript 8 Baseline a + (log Subscript 8 Baseline (b minus 4) minus 4 log Subscript 8 Baseline c)