Question

A pole, 4m high, stands, vertically, on

level ground. If the sun is at an angle of 30° to the horizontal,
how long is the shadow.

Use the tangent ratio to solve the problem.​

Answer 1

Length of the shadow of the pole is 6.93 metres

Explanation:

Given:

Height of the pole = 4 m

The angle sun makes with the horizontal = 30 degrees

To Find:

Length of the shadow of the pole = ?

Solution:

The tangent ratio is the value received when the length of the side opposite of angle theta is divided by the length of the side adjacent to angle theta

Let x be the length of the shadow

According to the tangent ratio

`tan {\theta} = (opposite)/(adjacent)`

On substituting the values,

`ta( {30^(o)) = (4)/(x)`

`x = \frac{4}{tan ({30^(o))}}`

`x =(4)/(0.57735027)`

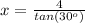
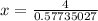
x = 6.93 m