Question

How would this problem be solved?

Answer 1

Explanation:

Do you still need help

Answer 2

The rectangular garden will require 128 ft of fencing.

Explanation:

Given:

Length of the rectangular field =
`32 \ ft`

Width of the rectangular garden =
`x \ ft`

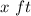
Side of square =
`x \ ft`

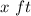
We need to find the fencing required to enclose the rectangular garden.

Solution:

We will first find the fencing required for the square.

Now fencing required of the square means we need to find the perimeter of the square.

Perimeter of the square is equal to sum of all sides.

framing in equation form we get;

Perimeter of square =
`x+x+x+x =4x`

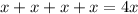
Now it has been given that;

gardener will need twice as much fencing to enclose the garden than it is used for square.

Perimeter of square =
`4x`

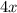
Twice the perimeter of square =
`4x*2 =8x`

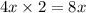
Now Perimeter of rectangular garden is given 2 times sum of length and width.

Perimeter of rectangular garden =
`2(32+x+x) =2(32+2x)=64+4x`

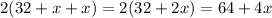
Now we know that Perimeter of rectangular garden is equal to Twice the perimeter of square.

so we can say that;

`64+4x=8x`

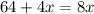
Combining the like terms we get;

`8x-4x=64\\\\4x =64`

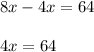
Dividing both side by 4 we get;

`(4x)/(4)=(64)/(4)\\\\x= 16\ ft`

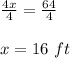
Now we will put the value of x in the Perimeter of garden we get;

Fencing required for the rectangular garden =
`64+4x =64+4* 16 = 64+64 = 128\ ft`

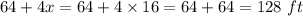
Hence The rectangular garden will require 128 ft of fencing.