Answer:
1)
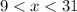
2)
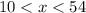
3) Not a triangle
4) This is a triangle
5)
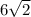
6)

7)
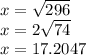
8)
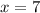
9) Obtuse
10) Obtuse
Explanation:
1) This one is a bit difficult to explain without a picture, but the third side needs to be longer than the difference of the 2 sides, and shorter than the sum of the 2 sides.
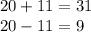
The third side must be shorter than 31 and longer than 9.
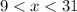
2) Same thing here.
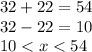
3) Use the same method as the first 2 questions.
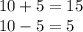
15 is greater than 5, but not less than 15. Not a triangle.
4) Same thing again.

12 is greater than 9.4 and less than 14.6. This is a triangle.
5) Split 72 into its prime factors, rewrite any pairs in exponent form, and apply

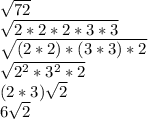
6) Same thing once again.
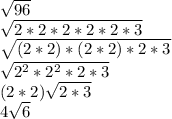
7) Use the pythagorean theorem (
 )
)
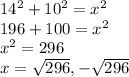
Distances cant be negative, so
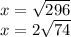
8) The time to repeat the same method has come.
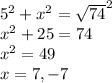
Distances cant be negative, so
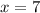
9) Check distances with the pythagorean theorem.
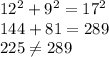
The third side is too long to be a right triangle, so this triangle is obtuse.
10) Repeat the previous method once more.
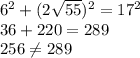
Third side is too long, triangle is obtuse.