Question

A 2.00 kg box slides on a rough, horizontal surface, hits a spring with a speed of 1.90 m/s and compresses it a distance of 10.0 cm before coming to rest. Determine the force constant (in N/m) of the spring, if the coefficient of kinetic friction between the block and the surface is μk = 0.660.

Answer 1

463.2 N/m

Step-by-step explanation:

mass of block, m = 2 kg

velocity of spring, v = 1.9 m/s

distance, r = 10 cm = 0.1 m

coefficient of friction, μ = 0.66

Let the spring constant is K.

friction force, f = μ mg = 0.66 x 2 x 9.8 = 12.94 N

Use work energy theorem

`(1)/(2)mv^(2)=f * r + (1)/(2)Kr^(2)`

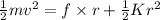
0.5 x 2 x 1.9 x 1.9 = 12.94 x 0.1 + 0.5 x K x 0.1 x 0.1

3.61 = 1.294 + 0.005 K

K = 463.2 N/m

Thus, the spring constant is 463.2 N/m.

Answer 2

Step-by-step explanation:

Given

mass of box
`m=2\ kg`

speed of box
`v=1.9\ m/s`

distance moved by the box
`x=10\ cm`

coefficient of kinetic friction
`\mu _k=0.66`

Friction force
`f_r=\mu_kN`

`f_r=0.66* mg`

`f_r=0.66* 2* 9.8=12.936 \N`

Kinetic Energy of box will be utilize to overcome friction and rest is stored in spring in the form of elastic potential energy

`(1)/(2)mv^2=f_r\cdot x+(1)/(2)kx^2`

`(1)/(2)* 2* 1.9^2=12.936* 0.1+(1)/(2)* k* (0.1)^2`

`3.61-1.2936=0.005* k`

`k=463.28\ N/m`