Answer:
Step-by-step explanation:
Calculate the distance between origin O
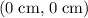 and the point
and the point
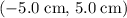 as follows:
as follows:
Substitute 0 cm for
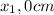 for
for
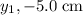 for
for
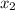 , and
, and
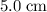 for
for
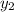 in
in
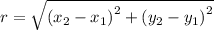
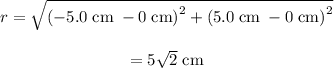
The electric field is,
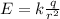
Substitute
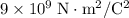 for k, 10 nC for q, and
for k, 10 nC for q, and
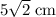 for r in
for r in
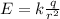
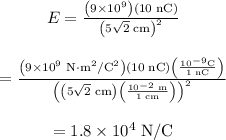
Therefore, the electric field at the position
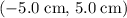 is
is
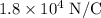
The electric field is inversely proportional to the square of the distance r.
The electric field in vector form is,
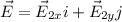
Here,
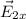 is the x component of electric field vector, and
is the x component of electric field vector, and
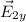 is the y component of electric field vector.
is the y component of electric field vector.
The x component of electric field vector is
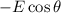 , and the y component of electric field vector is
, and the y component of electric field vector is
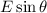 .
.
Substitute
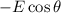 for
for
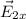 , and
, and
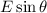 for
for
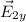 in
in
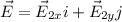
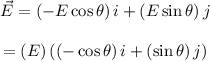
Substitute
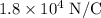 for E, and 450 for
for E, and 450 for
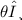 in
in
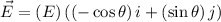
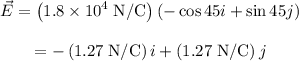
Therefore, the electric field vector in component form is,
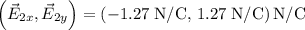
The point
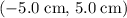 lies in the second quadrant, so the x component of electric field vector is negative, and y component of the electric field vector is positive
lies in the second quadrant, so the x component of electric field vector is negative, and y component of the electric field vector is positive