Question

Wildlife biologists inspect 140 deer taken by hunters and find 28 of them carrying ticks that test positive for Lyme disease.1) Create a 90% confidence interval for the percentage of deer that may carry such ticks. % 2) If the scientists want to cut the margin of error in half, how many deer must they inspect? 3) What concerns do you have about this sample?A. Since females and young deer are usually not hunted, this sample may not be representative of all deer. Also, since deer ticks are parasites and can easily be spread from one deer to another, the ticks may not be distributed evenly throughout the deer population. B. Since females and young deer are usually not hunted, this sample may not be representative of all deer. C. Since deer ticks are parasites and can easily be spread from one deer to another, the ticks may not be distributed evenly throughout the deer population. D. There are no concerns about this study.

Answer 1

1) he confidence interval boundaries are (14.44%, 25.56%).

2) n = 560

3) A. Since females and young deer are usually not hunted, this sample may not be representative of all deer. Also, since deer ticks are parasites and can easily be spread from one deer to another, the ticks may not be distributed evenly throughout the deer population.

Explanation:

We are given the following parameters:

n = 140; x = 28; c = 90% = 0.09

1) The sample proportion (p) = 28/140 = 0.2

In addition, 1 - α = 0.9; α = 0.1. We can determine
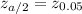`z_(a/2) = z_(0.05)` using the normal probability table. Thus:

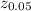`z_(0.05)` = 1.645

Then, the error margin (E) is:

E =
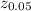`z_(0.05)`*sqrt[p(1-p)/n] = 1.645*sqrt[0.2(1-0.2)/140] = 0.0556

Thus, the confidence interval boundaries are:

p-E = 0.2 - 0.0556 = 0.1444 = 14.44%

p+E = 0.2+0.0556 = 0.2556 = 25.56%

2) From the formula for error margin, we can deduce that if the error margin is cut into half, the number of deer will be 4*140 = 560

3) The sample considered are for deer taken by hunters. In addition, deer with diseases are easily captured compared with those without disease. Thus, the sample is biased.