Answer:
Electrostatic force,

Number of electrons, n = 2681 electrons
Step-by-step explanation:
Given that,
Charges,
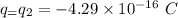
Separation between charges,
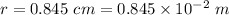
(a) Let F is the magnitude of the electrostatic force acting between them. The electric force between charges is given by :
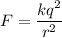
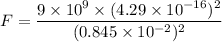

(b) Let n be the excess electrons on each drop, giving it its charge imbalance. It can be calculated using quantization of electric charge as :
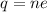
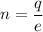
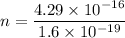
n = 2681.25 electrons
or
n = 2681 electrons
So, the number of excess electrons on each drop is 2681 electrons. Hence, this is the required solution.