Answer:
A)
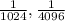
B)
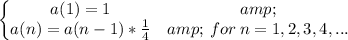
C)

Explanation:
1) Incomplete question. So completing the several terms:
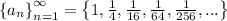
We can realize this a Geometric sequence, with the ratio equal to:
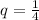
A) To find the next two terms of this sequence, simply follow multiplying the 5th term by the ratio (q):
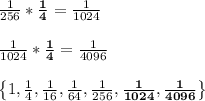
B) To find a recurrence a relation, is to write it a function based on the last value. So that, the function relates to the last value.
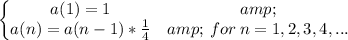
C) The explicit formula, is one valid for any value since we have the first one to find any term of the Geometric Sequence, therefore:
