Answer:
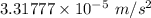


Step-by-step explanation:
G = Gravitational constant = 6.67 × 10⁻¹¹ m³/kgs²
 = Mass of Moon =
= Mass of Moon =
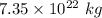
 = Mass of Sun =
= Mass of Sun =
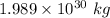
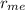 = Distance between Moon and Earth =
= Distance between Moon and Earth =
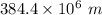
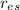 = Distance between Sun and Earth =
= Distance between Sun and Earth =
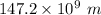
Acceleration due to gravity is given by

The magnitude of the acceleration due to gravity on the surface of Earth due to the Moon is
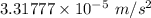
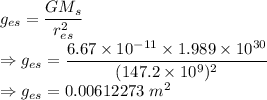
The magnitude of the acceleration due to gravity at Earth due to the Sun is

Dividing the equations we get

The acceleration due to gravity by the Sun is 184.54 times the acceleration of the Moon.
The Moon is still responsible for the tides because of there being a difference in the gravity exerted on Earth's near and far side.