Question

triangle is placed in a semicircle with a radius of 8cm, as shown below. Find the area of the shaded region. Use the value 3.14 for π, and do not round your answer. Be sure to include the correct unit in your answer.

Answer 1

Area of shaded region is
`36.48 \ cm^2`.

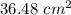Explanation:

We have drawn the diagram for your reference.

Given:

radius = 8 cm

Diameter is 2 times radius.

Diameter =
`2* 8 =16 \ cm`

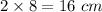
We need to find the Area of shaded region.

Solution:

First we will find the Area of Semicircle.

Now we know that Area of semicircle is half times π times square of radius.

framing in equation for we get;

Area of Semicircle =
`(1)/(2) * \pi * r^2 = (1)/(2) * \pi * 8^2=100.48\ cm^2`

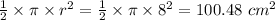
Now we will find the Area of Triangle.

Now base diameter of the semicircle and height is radius of the circle.

We know that Area of triangle is half times base times height.

framing in equation form we get;

Area of triangle =
`(1)/(2) * 16 * 8 = 64 \ cm^2`

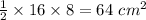
Now Area of the shaded region can be calculated by subtracting Area of triangle from Area of semicircle.

framing in equation form we get;

Area of the shaded region =
`100.48 - 64 = 36.48 \ cm^2`

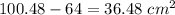
Hence Area of shaded region is
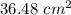`36.48 \ cm^2`.