Question

PLEASE HELP! Urgent

Answer 1

b.
`((3)/(2),-2)`

Explanation:

Given:

A triangle with coordinates A(-1, 0), B(-1, -4), and C(4, -4).

As clear from the graph the two legs of the triangle AB and BC are perpendicular to each other as BC is parallel to x-axis and AB is parallel to y-axis.

Therefore, the given triangle is a right angled triangle with right angle at B and AC as the hypotenuse.

Circumcenter is the center of a circle that passes through the three vertices of the given triangle.

Now, we know that, circumcenter of a right angled triangle always lies on the midpoint of its hypotenuse. Therefore, the circumcenter is the midpoint of line segment AC.

By midpoint formula, the midpoint of two points
`(x_1,y_1)\ and\ (x_2,y_2)` is given as:

Midpoint =
`((x_1+x_2)/(2),(y_1+y_2)/(2))`

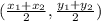
Therefore, the circumcenter for the points A(-1, 0) and C(4, -4) is given as:

Circumcenter =
`((-1+4)/(2),(0-4)/(2))=((3)/(2),(-4)/(2))=((3)/(2),-2)`

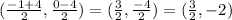
Therefore, the circumcenter of the given triangle is at the point
`((3)/(2),-2)`.

So, option (b) is correct.