Question

Biologists have noticed that the chirping of crickets of a certain species is related to temperature, and the relationship appears to be very nearly linear. A cricket produces 112 chirps per minute at 74 degrees Fahrenheit and 179 chirps per minute at 82 degrees Fahrenheit..

Answer 1

`T(N)=(67)/(8)N-(2031)/(4)`

Explanation:

Please consider the complete question.

Biologists have noticed that the chirping rate of crickets of a certain species is related to temperature, and the relationship appears to be very nearly linear. A cricket produces 112 chirps per minute 74° F at and 179 chirps per minute at 82°F. Find a linear equation that models the temperature T as a function of the number of chirps per minute N.

We have been given two points on the line
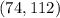`(74,112)` and
`(82,179)`.

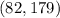First of all, we will find the slope of the line using given points as:

`\text{Slope}=m=(y_2-y_1)/(x_2-x_1)`

`m=(179-112)/(82-74)`

`m=(67)/(8)`

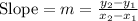
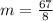
Now, we will points-slope form of an equation to write our required equation as:

`(y-y_1)=m-(x-x_1)`

`(y-112)=(67)/(8)-(x-74)`

`(y-112)=(67)/(8)(x-74)`

`y-112=(67)/(8)x-(67)/(8)*74`

`y-112+112=(67)/(8)x-(67)/(8)*74+112`

`y=(67)/(8)x-(67)/(4)*37+(4*112)/(4)`

`y=(67)/(8)x-(2479)/(4)+(448)/(4)`

`y=(67)/(8)x-(2031)/(4)`

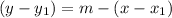
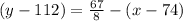
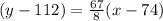
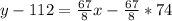
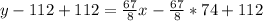
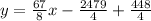
Since we are required to write temperature T as a function of the number of chirps per minute N, so we will get:

`T(N)=(67)/(8)N-(2031)/(4)`

Therefore, our required function would be
`T(N)=(67)/(8)N-(2031)/(4)`.