I believed here is the correct and complete question, and I'm going to work just on that.
117 grams of liquid water are in a cylinder with a piston maintaining 1 atm (101325 Pa) of pressure. It is exactly at the boiling point of water, 373.15 K. We then add heat to boil the water, converting it all to vapor.
The molecular weight of water is 18 g/mol and the latent heat of vaporization is 2260 J/g.
1) How much heat is required to boil the water?
2) Assume that the liquid water takes up approximately zero volume, and the water vapor takes up some final volume Vf. You may also assume that the vapor is an ideal gas. How much work did the vapor do pushing on the piston?
3) How much did the water internal energy change?
Answer:
1) Q = 264.420 KJ
2) W = 20.16KJ
3) ΔU = 244.26KJ
Step-by-step explanation:
Let's state the parameters given.
Given that:
mass (m) = 117 gram
specific latent heat of vaporization (L) = 2260 J/g
Pressure (P) = 1 atm or 101325 Pa
Temperature (T) = 373.15 K
molecular weight = 18 g/mol
1).
How much heat is required to boil the water
i.e we are to find the heat energy which is denoted by Q = mL
Q = 117g × 2260 J/g
= 264420 J
= 264.42 KJ
2).
Assume that the liquid water takes up approximately zero volume:
i.e
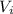 = 0
= 0
and the water vapor takes up some final volume
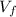
If we assume that the vapor is an ideal gas.
We can represent the parameters using the equation of an ideal gas:
PV=nRT
where;
P = 1 atm or 101325 Pa
V = ??? (unknown)
n = no of moles of the water
n = mass/molecular weight
= 117/18
= 6.5 mole
R = 8.314
T = 373.15
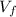 =
=
![(nRT)/(P)</p><p>[tex]V_f](https://img.qammunity.org/2021/formulas/physics/high-school/5n1n72yj2y8qlgkhkcx2bczi6pw49lx8qh.png) =
=
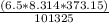
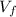 = 0.199 m³
= 0.199 m³
Don't forget the question number to say "How much work did the vapor do pushing on the piston"?
Now; at Constant Pressure, the work done by the vapour in pushing on the piston can be calculated as:
W =
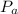 (ΔV)
(ΔV)
=

= 101.325 × (0.199 - 0)
= 101.325 × 0.199
= 20.16KJ
3).
How much did the water internal energy change?
let ΔU = water internal energy change
Q = Heat Energy
W = work done by the vapour in pushing on the piston
Q = ΔU + W
ΔU = - Q + W (by multiplying the left hand side with minus (-))
ΔU = Q - W
ΔU = 264.42 - 20.16
ΔU = 244.26KJ