Question

Research has suggested that musicians process music in the same cortical regions in which adolescents process algebra. When taking introductory algebra, will students who were enrolled in formal instrumental or choral music instruction during middle school outperform those who experienced neither of these modes of musical instruction? The sample consisted of 6026 ninth-grade students in Maryland who had completed introductory algebra. Of these, 3239 students had received formal instrumental or choral instruction during all three years of middle school, while the remaining students had not. Of those receiving formal musical instruction, 2818 received a passing grade on the Maryland Algebra/Data Analysis High School Assessment (HSA). In contrast, 2091 of the 2787 students not receiving musical instruction received a passing grade.Is there a significant difference in the proportions of students with and without musical instruction who receive a passing grade on the Maryland HSA? State hypotheses, find the test statistic, and use software or the bottom row of Table C to get a P-value.a. an observed difference is 0.12 and P > 0.0002b. an observed difference is 0.13 and P > 0.0001c. an observed difference is 0.12 and P < 0.0001d. an observed difference is 0.13 and P > 0.0002

Answer 1

c. an observed difference is 0.12 and P < 0.0001

Explanation:

Let p1 be the proportion of the students who received musical instruction received a passing grade

Let p2 be the proportion of the students who didn't receive musical instruction received a passing grade

Null and Alternative hypotheses are:

• 
  `H_(0)`: p1-p2=0

• 
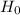  `H_(a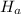)`: p1-p2≠0

Test statistic can be found using the equation:

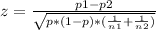`z=\frac{p1-p2}{\sqrt{{p*(1-p)*((1)/(n1) +(1)/(n2)) }}}` where

• p1 is the sample proportion of the students who received musical instruction received a passing grade (
  `(2818)/(3239) =0.87`)

• p2 is the sample proportion of the students who didn't receive musical instruction received a passing grade (
  `(2091)/(2787) =0.75`)

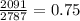• p is the pool proportion of p1 and p2 (
  `(2818+2091)/(6026)=0.81`)

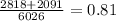• n1 is the sample size of the students who received musical instruction (3239)

• n2 is the sample size of the students who didn't receive musical instruction (2787)

Thus,
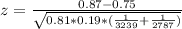`z=\frac{0.87-0.75}{\sqrt{{0.81*0.19*((1)/(3239) +(1)/(2787)) }}}` ≈ 11.84 gives p-value < 0.0001

Observed difference is: 0.87-0.75=0.12