Question

Suppose x and y are nonzero vectors in an inner product space. Show that x and y are orthogonal if and only if ||x+y|| = ||x-y||

Answer 1

Explanation:

Suppose x and y are nonzero vectors in an inner product space.

Let us assume that x and y are orthogonal

i.e. innter product is 0.

This implies dot product of x and y is 0

Then x.y =0

i.e.
`x^2+y^2 +2x.y = x^2+y^2-2x.y\\||x+y||=||x-y||`

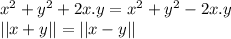
Proved

Converse part:

Let
`||x+y||=||x-y||`

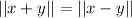
Square also would be equal

`||x+y||^2=||x-y||^2\\||x||^2+||y||^2+2x,t=||x||^2+||y||^2-2x.y\\x.y =0`

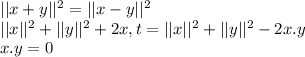
Hence inner product of x and y is 0