Answer:
Step-by-step explanation:
a)

There will be no x-component as it is acting on y-axis completely
b)
y-component will be the total force
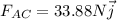 as found earlier
as found earlier
c)
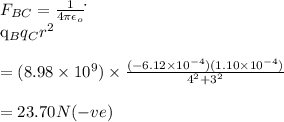
d)
x-component of
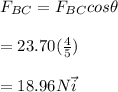
e)
y-component of
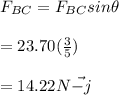
f)
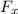 =(x-component of
=(x-component of
![F_(AC))+(x-component of [tex]F_(BC)](https://img.qammunity.org/2021/formulas/physics/college/qg7l67v8lw2op2z85uxynzj822rai3vs4f.png) )
)
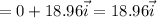
g)

h)
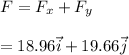

from +ve x axis counter clockwise.