Question

(a) The position of a particle at time t is s(t) = t^3 + t. Compute the average velocity over the time interval [7, 12].(b) Estimate the instantaneous velocity at t = 7. (Round your answer to the nearest whole number)

Answer 1

The average velocity of the particle over the interval [7, 12] is 278 m/s. The estimated instantaneous velocity at t = 7, after rounding to the nearest whole number, is 148 m/s.

Step-by-step explanation:

Calculating Average Velocity and Estimating Instantaneous Velocity

To calculate the average velocity of a particle given by the position function
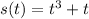`s(t) = t^3 + t`over the time interval [7, 12], we'll use the formula

Average velocity = ∆s/∆t = (s(12) - s(7))/(12 - 7)

First, we find s(12) and s(7):

`s(12) = 12^3 + 12 = 1728 + 12 = 1740 \\ s(7) = 7^3 + 7 = 343 + 7 = 350`

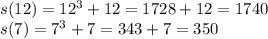
So, the average velocity = (1740 - 350)/5 = 1390/5 = 278 m/s.

For estimating the instantaneous velocity at t = 7, we find the derivative of the position function to obtain the velocity function:

`v(t) = 3t^2 + 1`

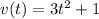
Then we substitute t = 7 into the velocity function:

`v(7) = 3(7)^2 + 1 = 3(49) + 1 = 148 m/s`

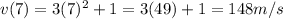
After rounding to the nearest whole number, the estimated instantaneous velocity at t = 7 is 148 m/s.

Answer 2

a) Average velocity = 278 units

b) Instantaneous velocity at t = 7 seconds is 148 units

Step-by-step explanation:

a) Average velocity is the ratio of displacement to time.

We have

s(t) = t³ + t

t is in between 7 and 12

s(7) = 7³ + 7 = 350

s(12) = 12³ + 12 = 1740

Displacement = 1740 - 350 = 1390

Time = 12 - 7 = 5

Displacement = Average velocity x time

1390 = Average velocity x 5

Average velocity = 278 units

b) s(t) = t³ + t

Differentiating

v(t) = 3t² + 1

At t = 7

v(t) = 3 x 7² + 1 = 148 units

Instantaneous velocity at t = 7 seconds is 148 units