The current rotational period of that star is 10.01 hours.
Step-by-step explanation:
Given that,
Initial angular velocity of the star,

It decelerates, final angular speed,
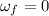
Deceleration,
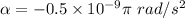
It is not required to use the rotational kinematics formula. The angular velocity in terms of time period is given by :
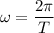
T is current rotational period of that star
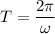
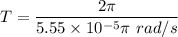
T = 36036.03 second
or
1 hour = 3600 seconds
So, T = 10.01 hours
So, the current rotational period of that star is 10.01 hours. Hence, this is the required solution. Hence, this is the required solution.