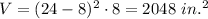Answer:
Explanation:
Given
square bottom area is
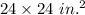
Suppose x in. is cut from each corner to make a open box with maximum volume
New base area is
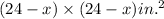
Volume of box
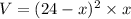
Differentiate V w.r.t x to get maximum volume
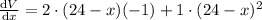
Put
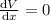
![\left ( 24-x\right )\left [ -2x+24-x\right ]=0](https://img.qammunity.org/2021/formulas/mathematics/high-school/xag0kpp88sblfy5c0qzydknlk4mr4abp6t.png)
![\left ( 24-x\right )\left [ 24-3x\right ]=0](https://img.qammunity.org/2021/formulas/mathematics/high-school/xzrnhylld1wnvrzs2kyh352rf4eyer4f8a.png)

but x=24 is not possible therefore x=8 will yield maximum volume