Question

A bridge in the shape of an arch connects two cities separated by a river. The two ends of the bridge are located at (–7, –13) and (7, –13), and the center of the arch on the bridge is located at (0, 0). Find the equation of the arch of the bridge.

Answer 1

`y=-(13)/(49)x^2`

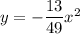
Explanation:

The shape of an arch corresponds to a parabola.

the general equation for a parabola is:

`y=ax^2+bx+c`

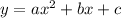
we're given three coordinates: (-7,-13),(7,-13) and (0,0)

so we can plug these values in the general equation to make 3 separate equations:

(x,y) = (-7,-13)

`-13=a(-7)^2+b(-7)+c`

`49a-7b+c=-13`

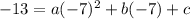
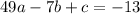
(x,y) = (7,-13)

`-13=a(7)^2+b(7)+c`

`49a+7b+c=-13`

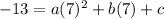
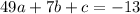
(x,y) = (0,0)

`0=a(0)^2+b(7)+c`

`c=0`

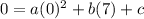
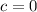
so we have three equations. and we can solve them simultaneously to find the values of a,b, and c.

we've already found c = 0, let's use substitute it to other equations.

`49a-7b+c=-13\quad\Rightarrow\quad49a-7b=-13`

`49a+7b+c=-13\quad\Rightarrow\quad49a+7b=-13`

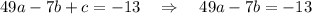
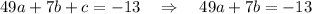
we can solve these two equation using the elimination method, by simply adding the two equations

`\quad\quad49a-7b=-13\\+\quad49a+7b=-13`

------------------------------

`\quad\quad 98a=-26`

`\quad\quad a=-(13)/(49)`

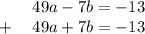
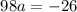
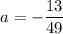
Now we can plug this value of a in any of the two equations.

`49a-7b=-13`

`49\left(-(13)/(49)\right)-7b=-13`

`-13-7b=-13`

`-7b=0`

`b=0`

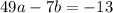
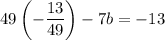
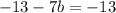
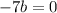
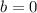
We have the values of a,b, and c. We can plug them in the general equation to find the equation of the arch.

`y=\left(-(13)/(49)\right)x^2+0x+0`

`y=-(13)/(49)x^2`

`49y=-13x^2`

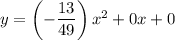
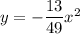
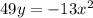
This our equation of the arch!