Question

Show that the equation represents a circle by rewriting it in standard form, and find the center and radius of the circle.

x^2 + y^2 - 2x + 8y + 1 = 0
standard form
center (x, y) = ( )
radius

Answer 1

center is (1,-4)

radius is 4

Explanation:

`x^2 + y^2 - 2x + 8y + 1 = 0`

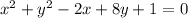
standard form is

`(x-h)^2+(y-k)^2=r^2`, where center is (h,k) and r is the radius

apply completing the square method to get standard form

`(x^2 - 2x )+(y^2+ 8y)=-1`

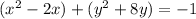
take half of the middle term and square it and then add it on both sides

`(x^2 - 2x+1 )+(y^2+ 8y+16)=-1+1+16`

`(x^2-1)^2+(y^2+4)^2=16`

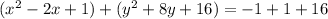
center is (1,-4) and r^2 is 16

radius is 4