Question

The pilot of an aircraft wishes to fly due west in a wind blowing at 45 km/h toward the south. If the speed of the aircraft in the absence of wind is 165 km/h, in what direction (in degrees) should the aircraft head? Use the counter-clockwise from east convention.

Answer 1

164.2°

Step-by-step explanation:

speed of wind (w) = 45 km/h due south

speed of aircraft (a) = 165 km/h

in what direction (in degrees) should the aircraft head in so as to fly due west?

To get the direction the pilot should fly, we can form a triangle with the data available where

• the direction of the wind (due south) serves as the opposite side
• the direction the pilot would have to fly so he can end up at he west serves as the hypothenuse
• θ is the angle between the direction the pilot would have to fly and the direction the pilot wishes to fly.
• the direction the pilot wishes to fly ( west) will serve as the adjacent side
• all this can be seen from the attached diagram.

now sin θ =
`(speed of the wind)/(speed of the aircraft)`

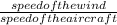
sin θ =
`(45)/(165)`

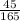
θ =
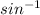`sin^(-1)` 0.2728

θ = 15.8°

since we are to use the counter-clockwise from east convention our measurement would have to be taken anticlockwise from the east direction, therefore the direction of the aircraft (Ф) = 180-15.8 = 164.2°