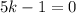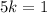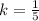Question

Find all values of the scalar k for which the two vectors are orthogonal:

u = (2,3) and v= (k+1, k-1)

Answer 1

`k = (1)/(5)`

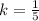
Explanation:

Two vectors are said to be orthogonal if their dot product is zero.

Dot product:

Suppose we have two vectors, a and b.

a = (1,2)

b = (2,3)

Their dot product is:

a.b = (1,2).(2,3) = 1*2 + 2*3 = 8

In this problem:

u = (2,3)

v = (k + 1, k - 1)

So

u.v = (2,3).(k + 1, k - 1) = 2(k + 1) + 3(k - 1) = 2k + 2 + 3k - 3 = 5k - 1

For the vectors to be orthogonal, the dot product has to be 0. So:

`5k - 1 = 0`

`5k = 1`

`k = (1)/(5)`