Question

1. You can do 90 sit-ups in 2 minutes. Your friend can do 135 sit-ups in 3 minutes. Do these rates form a proportion? Explain

2. The ratio of quarters to dimes in a coin collection is 5:3. You add the same number of new quarters as dimes to the collection.
a. Is the ratio of quarters to dimes still 5:3?
b. If so, illustrate with an example. If not, give a counter-example.
3. You are 13 years old, and your cousin is 19 years old. As you grow older, is your age proportional to your cousin's age? Explain your reasoning

Answer 1

1. The relation is proportional.

2. The ratio of quarters and to dimes will not remain 5 : 3.

3. y = 6 + x, Hence, not proportional.

Explanation:

1. I can do 90 sit-ups in 2 minutes and my friend can do 135 sit-ups in 3 minutes.

If we consider t as the time in minutes and n as the number of sit-ups, then we can write (2,90) and (3,135) as two ordered pairs.

So, the relation between t and n will be

`(n - 135)/(135 - 90) = (t - 3)/(3 - 2)`

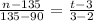
⇒ n = 45t

Therefore, the relation is proportional.

2. The initial ratio of quarters to dimes was 5:3. If I add the same number of quarters and dimes to it then,

a) The ratio of quarters and dimes will not still be 5 : 3.

b) Let, the number of quarters was 5 then the number of dimes was 3. {As the ratio was 5 : 3}

Now, we add 3 new quarters and 3 new dimes in the collection. then, finally, the number of quarters will be (5 + 3) = 8 and the number of dimes will become (3 + 3) = 6.

Therefore, the new ratio will become 8 : 6 = 4 : 3 which is not equal to 5 : 3.

3. I am 13 years old, and my cousin is 19 years old.

So, if my age is given by x and that of my cousin is y, then

y - x = 19 - 13

⇒ y - x = 6

⇒ y = 6 + x

This relation will continue as the year passes. So, the relation is not proportional as the relation is not like y = kx. (Answer)