Question

A publisher reports that 79% of their readers own a laptop. A marketing executive wants to test the claim that the percentage is actually more than the reported percentage. A random sample of 350 found that 82% of the readers owned a laptop. Is there sufficient evidence at the 0.01 level to support the executive's claim?

Answer 1

There is sufficient evidence at the 0.01 level to support the executive's claim

Explanation:

Given that a publisher reports that 79% of their readers own a laptop. A marketing executive wants to test the claim that the percentage is actually more than the reported percentage

Sample size n =350

Sample proportion P =0.82

`H_0: p = 0.79\\H_a: p >0.79`

(right tailed test at 1% level of significance for proportions)

Assuming H0 to be true i.e. p = 0.79, std error of sample proporiton

=
`\sqrt{(0.79*0.21)/(250) } \\=0.02576\\`

p difference =
`0.82-0.79=0.03`

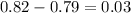
test statistic Z=p diff/std error

=1.1646

p value = 0.1221

Since p value >0.01, our significant value, we fail to reject H0

There is sufficient evidence at the 0.01 level to support the executive's claim