Question

If an integer is to be randomly selected from set M above and an integer is to be randomly selected from set T above, what is the probability that the product of the two integers will be negative?

A. 0
B. 1/3
C. 2/5
D. 1/2
E. 3/5

Answer 1

D.
`(1)/(2)`

Explanation:

Given:

Set M = {-6, -5, -4, -3, -2}

Set T = {-2, -1, 0, 1, 2, 3}

Now, the product of two numbers is negative only if the numbers choses are of opposite sign.

A negative number is a number less than 0. A positive number is a number greater than 0.

So, the set M has all numbers as negative.

Set T has 2 negative and 4 positive numbers.

Now, probability of choosing a negative number from set M is 1 as all the numbers are negative. So,

`P(negative)=1`

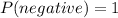
Now, we need to find the probability of choosing a positive number from set T.

Set T has 3 positive numbers out of total 6 numbers.

Therefore, the probability of choosing a positive number from set T is given as:

`P(positive)=\frac{\textrm{Number of positive numbers}}{\textrm{Total number}}\\\\P(positive)=(3)/(6)=(1)/(2)`

Therefore, the probability that the product of the two integers will be negative is obtained by the product of the individual probabilities. This gives,

`P(negative\ product)=P(positive)\cdot P(negative)\\\\P(negative\ product)=(1)/(2)\cdot 1=(1)/(2)`

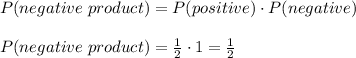
Therefore, the correct answer is option D.