Question

A student sells small and large greeting cards decorated with kirigami at the craft fair.The small cards cost $3 per card ,and the large card cost $5 per card.The student collects $95 for selling a total of 25 cards.How many of each type of card did the student sell?​

Answer 1

y = 25 - 15

y = 10

Explanation:

Answer 2

The student sold 15 small cards and 10 large cards

Solution:

Let "x" be the number of small cards sold

Let "y" be the number of large cards sold

cost of 1 small card = $ 3

cost of 1 large card = $ 5

They sold a total of 25 cards

Therefore, a equation is framed as:

number of small cards sold + number of large cards sold = 25

x + y = 25

y = 25 - x ---------- eqn 1

The student collects $95. Therefore, a equation is framed as:

number of small cards sold x cost of 1 small card + number of large cards sold x cost of 1 large ca = 95

`x * 3 + y * 5 = 95`

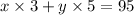
3x + 5y = 95 ---------- eqn 2

Substitute eqn 1 in eqn 2

3x + 5(25 - x) = 95

3x + 125 - 5x = 95

-2x = 95 - 125

-2x = -30

x = 15

Substitute x = 15 in eqn 1

y = 25 - 15

y = 10

Thus student sold 15 small cards and 10 large cards