Question

Consider two point charges located on the x axis: one charge, q1 = -11.5nC , is located at x1 = -1.685m ;the second charge, q2 = 40.0nC , is at the origin (x=0.0000).

What is the net force exerted by these two charges on a third charge q3 = 55.0nC placed between q1 and q2 at x3 = -1.195m ?

Your answer may be positive or negative, depending on the direction of the force.

Answer 1

`F_(t3)=-3.76\ 10^(-5)\ N`

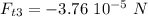
The net force is pointed to the left side

Step-by-step explanation:

Electrostatic Force

The formula to compute the electrostatic force between two point charges was introduced by Charles Coulomb and it's expressed as

`\displaystyle F=(k\ q_1\ q_2)/(r^2)`

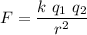
Where q1 and q2 are the magnitudes of the charges, r is the distance between them and k is a proportionality constant

The data provided in the problem is

`\displaystyle x_1=-1,685\ m`

`\displaystyle q_1=-11.5\ nC`

`\displaystyle q_2=40\ nC`

`\displaystyle q_3=55\ nC`

`\displaystyle x_3=-1.195\ m`

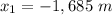
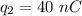
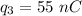
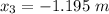
The distance between the charge 1 and 3 is

`\displaystyle d_(13)=1.685-1.195`

`\displaystyle d_(13)=0.49\ m`

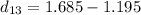
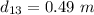
The distance between charges 2 and 3 is

`\displaystyle d_(23)=1.195\ m`

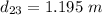
Now, let's compute the force exerted by q1 on q3

`\displaystyle F_(13)=(k\ q_1\ q_3)/(d_(13)^2)`

`\displaystyle F_(13)=(9\ 10^9\ 11.5\ 10^(-9)\ 55\ 10^(-9))/(0.49^2)`

`\displaystyle F_(13)=2.37\ 10^(-5)\ N`

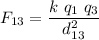
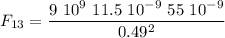
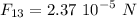
This value is the scalar magnitude of the force, we'll take care of the directions later. The force by q2 on q3 is

`\displaystyle F_(23)=(k\ q_2\ q_3)/(d_(23)^2)`

`\displaystyle F_(23)=(9\ 10^(9)\ 40\ 10^(-9)\ 55\ 10^(-9))/(1.195^2)`

`\displaystyle F_(23)=1.39\ 10^(-5)\ N`

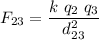
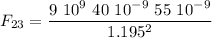
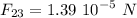
Given that q1 is negative and q3 is positive, q1 attracts q3 to the left, so F13 is in the negative direction. The charge q2 is positive and repels q3 to the left, thus F23 is also negative. This leads us to compute the total force on q3 as

`\displaystyle F_(t3)=-F_(13)-F_(23)`

`\boxed{F_(t3)=-3.76\ 10^(-5)\ N}`

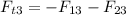
The net force is pointed to the left side