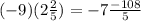Question

Catron evaluates the expression (negative 9) (2 and two-fifths) using the steps below.

Step 1: (Negative 9) (2 + two-fifths)
Step 2: (Negative 9) (Negative 2) + (negative 9) (two-fifths)
Step 3: Negative 18 + (negative 9) (two-fifths)
Step 4: (negative 27) (two-fifths)
Solution: Negative StartFraction 54 over 5 EndFraction = Negative 10 and four-fifths

Which describes Catron’s error?
She incorrectly broke up 2 and two-fifths.
She incorrectly distributed the –9; she should have distributed 2.
She did not follow order of operations.
She incorrectly converted from an improper fraction to a mixed number.

Answer 1

Catron'error is that She incorrectly broke up 2 and two-fifths.

Explanation:

Following Catron steps we have:

`-9(2 + (2)/(5) )\\-9(-2) + (-9)((2)/(5) )\\-18 + (-9)((2)/(5) )\\-27((2)/(5) )\\-(54)/(5) = - 10(4)/(5)`

Catron did not represent the problem correctly.

The correct step is:

`-9(2 (2)/(5) )\\-9((10 + 2)/(5) )\\-9((12)/(5) )\\-((108)/(5) )\\= - 21(3)/(5)`

Answer 2

Catron's error is

"She did not follow order of operations"

Explanation:

Catron evaluates the expression (negative 9) (2 and two-fifths)

That expression can be written as below

`(-9)(2(2)/(5))`

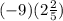
Catron's error is

"She did not follow order of operations"

The corrected steps are

Step1: Given expression is
`(-9)(2(2)/(5))`

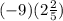
Step2: Convert mixed fraction into improper fraction

`(-9)(2(2)/(5))=(-9)((12)/(5))`

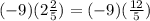
Step3: Multiplying the terms

`(-9)(2(2)/(5))=-7(-108)/(5)`

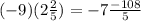
Therefore solution
`(-9)(2(2)/(5))=-7(-108)/(5)`