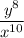Please help answer the question.

Question

asked Oct 25, 2021 164k views

1 Answer

Rok Benko · Answer 1 · 2021-10-29T03:29:50+0000

Answer:

a.
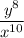
(y^8)/(x^(10))

Explanation:

First step is ti distribute the exponent outside the parenthesis. According to the law of exponents, you need to distribute it to each variable.

$\left((x^(-4)y)/(x^(-9)y^5)\right)^(-2)\\\\=(x^((-4*-2))y^((1*-2)))/(x^((-9*-2))y^((5*-2)))\\\\=(x^(8)y^(-2))/(x^(18)y^(-10))$

Now again, following the law of exponents, if you have negative exponents, you put them in the opposite side of the fraction.

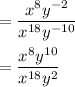
$=(x^8y^(-2))/(x^(18)y^(-10))\\\\=(x^8y^(10))/(x^(18)y^(2))\\\\$

Next, when it comes to division, we subtract the exponents of the numerator and the denominator of similar variables.

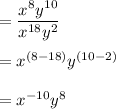
$=(x^8y^(10))/(x^(18)y^(2))\\\\=x^((8-18))y^((10-2))\\\\=x^(-10)y^8$

Since the exponent of x is negative, we move it below the fraction.

(y^8)/(x^(10))