Question

A regular square pyramid has base edges of length 16 and its lateral faces are inclined 30­° to the base of the pyramid. What is the (1) height of the pyramid (2) volume of the pyramid?

Answer 1

(1) 13.86 units.

(2) 1182.72 cubic units.

Explanation:

Please find the attachment.

We have been given that a regular square pyramid has base edges of length 16 and its lateral faces are inclined 30­° to the base of the pyramid.

(1) We can find height of pyramid using tan.

`\text{tan}=\frac{\text{Opposite}}{\text{Adjacent}}`

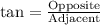
The length of opposite side will half the length of square base.

`(16)/(2)=8`

`\text{tan}(30^(\circ))=(8)/(h)`

`h=\frac{8}{\text{tan}(30^(\circ))}`

`h=13.8564064605420367`

`h\approx 13.86`

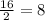
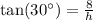
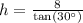
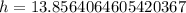
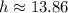
Therefore, the height of the pyramid will be 13.86 units.

(2). We know that volume of pyramid is 1/3 the product of base area and height.

`V=(1)/(3)*bh`

`V=(1)/(3)*16*16*13.86`

`V=(1)/(3)*3548.16`

`V=1182.72`

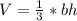
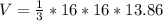
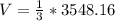
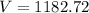
Therefore, the volume of the pyramid would be 1182.72 cubic units.