Question

A motorboat accelerates uniformly from a velocity of 6.5 m/s west to a velocity of 1.5 m/s west. If its acceleration was 2.7 m/s2 to the east, what is the displacement

of the motorboat during the acceleration?

Answer 1

The motorboat ends up 7.41 meters to the west of the initial position

Step-by-step explanation:

Accelerated Motion

The accelerated motion describes a situation where an object changes its velocity over time. If the acceleration is constant, then these formulas apply:

`\vec v_f=\vec v_o+\vec a.t`

`\displaystyle \vec r=\vec v_o.t+(\vec a.t^2)/(2)`

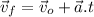
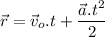
The problem provides the conditions of the motorboat's motion. The initial velocity is 6.5 m/s west. The final velocity is 1.5 m/s west, and the acceleration is
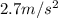`2.7 m/s^2` to the east. Since all the movement takes place in one dimension, we can ignore the vectorial notation and work with the signs of the variables, according to a defined positive direction. We'll follow the rule that all the directional magnitudes are positive to the east and negative to the west. Rewriting the formulas:

`v_f=v_o+a.t`

`\displaystyle x=v_o.t+(a.t^2)/(2)`

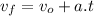
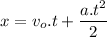
Solving the first one for t

`\displaystyle t=(v_f-v_o)/(a)`

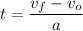
We have

`v_o=-6.5,\ v_f=-1.5,\ a=2.7`

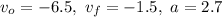
Using these values

`\displaystyle t=(-1.5+6.5)/(2.7)=1.852\ s`

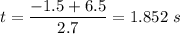
We now compute x

`\displaystyle x=(-6.5)(1.852)+((2.7)(1.852)^2)/(2)`

`x=-7,41\ m`

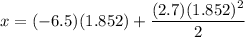
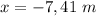
The motorboat ends up 7.41 meters to the west of the initial position