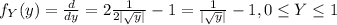Question

Let X be a continuous random variable with density functionf(x)={1−|x|0 for −1

Answer 1

`f_Y (y) =(d)/(dy) = 2 (1)/(2 |√(y)|) -1 = (1)/(|√(y)|) -1,0 \leq Y\leq 1`

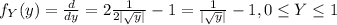
Explanation:

For this case we want to find the density function for
`Y=X^2`

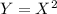
And we have the following density function for the random variable X:

`f(X) = 1- |X|,-1 \leq X \leq 1`

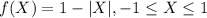
So we can do this replacing
`Y=X^2`

`F_Y (Y \leq y) = P(X^2 \leq y)`

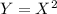
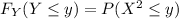
If we apply square root on both sides we got:

`P(-√(y) \leq X \leq √(y)) = \int_(-√(y))^0 1+t dt +\int_(0)^(√(y)) 1-t dt`

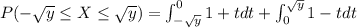
And if we integrate we got this:

`F_Y (y) = [t+ (t^2)/(2)] \Big|_(-√(y))^0+ [t -(t^2)/(2)] \Big|_(0)^(√(y))`

And replacing we got:

`F_Y (y) = [0 -(-√(y) +(y)/(2))] + [√(y) -(y)/(2)]`

`F_Y (y) = 2 |√(y)| -y`

And if we want to find the density function we just need to derivate the pdf like this:

`f_Y (y) =(d)/(dy) = 2 (1)/(2 |√(y)|) -1 = (1)/(|√(y)|) -1,0 \leq Y\leq 1`