Question

A 4.8 kg block is suspended from a spring with a spring constant of 500 N/m. A 50 g bullet is fired into the block from directly below with a speed of 130 m/s and is embedded in the block. (a) Find the amplitude of the resulting simple harmonic motion. m (b) What fraction of the original kinetic energy of the bullet appears as mechanical energy in the harmonic oscillator?

Answer 1

The fraction of the original kinetic energy of the bullet appears as mechanical energy in the harmonic oscillator is 0.00468.

Step-by-step explanation:

Given that,

Mass of block = 4.8 kg

Mass of bullet = 50 g

Spring constant = 500 N/m

Speed of bullet = 130 m/s

(a). We need to calculate the velocity

Using conservation of momentum

`m_(b)v_(b)=(m+m_(b))v`

`v=(m_(b)v_(b))/((m+m_(b)))`

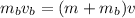
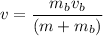
Put the value into the formula

`v=(0.05*130)/(4.8+0.05)`

`v=1.340\ m/s`

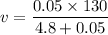
We need to calculate the amplitude of the resulting simple harmonic motion

Using formula energy

`(1)/(2)(m+m_(b))v_(1)^2=(1)/(2)kx^2`

Put the value into the formula

`(4.8+0.05)*1.340=500x^2`

`x^2=(4.8+0.05)/(500)`

`x=\sqrt{(4.8+0.05)/(500)}`

`x=0.0984\ m`

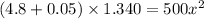
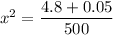
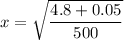
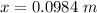
(b). We need to calculate the kinetic energy

Using formula of kinetic energy

`K.E=(1)/(2)*0.05*(130)^2`

`K.E=0.0423\ J`

`K.E=(1)/(2)mv^2+mgh`

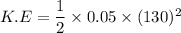
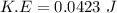
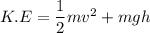
for harmonic oscillator,

`K.E=(1)/(2)*(4.8+0.05)*(1.340)^2+(4.8+0.05)*9.8*0.0984`

`K.E=9.031\ J`

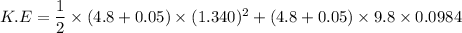
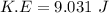
The fraction of the original kinetic energy of the bullet appears as mechanical energy in the harmonic oscillator

`(K.E_(b))/(K.E)=(0.0423)/(9.031)`

`(K.E_(b))/(K.E)=0.00468`

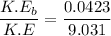
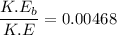
Hence, The fraction of the original kinetic energy of the bullet appears as mechanical energy in the harmonic oscillator is 0.00468.