Answer:
Option 2.
Explanation:
It is given that
a = <6,-9,3>
We need to compare the maginitude of vertor a and vector 4a.
If a vector is defined as v = <x,y,z>, then its magnitude is defined as
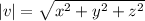
Using the above formula we get
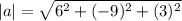
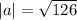
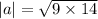
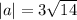
The vector 4a is
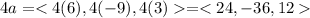
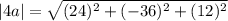
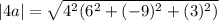
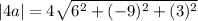
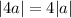
The magnitude of 4a is a factor of 4 greater than the magnitude of a.
Therefore, the correct option is 2.