Question

Suppose you are at the center of a large freely-rotating horizontal turntable in a carnival funhouse. As you crawl toward the edge, the angular momentum of you and the turntable:

a. decreases.
b. increases.
c. remains the same, but the RPMs decrease.
d. decreases in direct proportion to your decrease in RPMs.
e. none of these

Answer 1

c. remains the same, but the RPMs decrease.

Step-by-step explanation:

Because there aren't external torques on the system composed by the person and the turntable it follows that total angular momentum (I) is conserved, that means the total angular momentum is a constant:

`\overrightarrow{L}=constant`

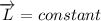
The total angular momentum is the sum of the individual angular momenta, in our case we should sum the angular momentum of the turntable and the angular momentum of a point mass respect the center of the turntable (the person)

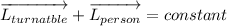`\overrightarrow{L_(turnatble)}+\overrightarrow{L_(person)}=constant` (1)

The angular momentum of the turntable is:

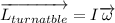`\overrightarrow{L_(turnatble)}=I\overrightarrow{\omega}` (2)

with I the moment of inertia and ω the angular velocity.

The angular momentum of the person respects the center of the turntable is:

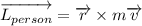`\overrightarrow{L_(person)}=\overrightarrow{r}* m\overrightarrow{v}` (3)

with r the position of the person respects the center of the turntable, m the mass of the person and v the linear velocity

Using the fact
`v=\omega r`:

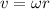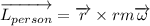`\overrightarrow{L_(person)}=\overrightarrow{r}* rm\overrightarrow{\omega}`(3)

By (3) and (2) on (1) and working only the magnitudes (it's all that we need for this problem):

`I\omega+r^(2)m\omega=constant`

`\omega(I+r^(2)m)=constant`

Because the equality should be maintained, if we increase the distance between the person and the center of the turntable (r), the angular velocity should decrease to maintain the same constant value because I and m are constants, so the RPM's (unit of angular velocity) are going to decrease.